Grafikus egyszerűsítésre
a Karnaugh-táblás egyszerűsítést tanuljuk. Előnye, hogy gyorsabb, biztosabban
jó eredményt adó, kevesebb munkát igénylő módszer. Hátránya, hogy legfeljebb
4 (esetleg 5) változóig használható, addig áttekinthető, könnyen használható,
addig áttekinthető, könnyen kezelhető. Azt már tudjuk a Karnaugh tábláról,
hogy az igazságtáblázat “célszerűen átalakított” változata. Ez a célszerűség
abban van, hogy az egyszerűsítési lehetőségek szinte ránézésre nyilvánvalóvá
válnak. A változókat a tábla szélein tüntetjük
fel, és a hozzájuk tartozó 0 illetve 1 értékek a mellettük lévő sorokra,
ill. oszlopokra vonatkoznak.
Így minden változó kombinációnak koordináta
rendszer-szerűen egy-egy elemi négyzetet feleltetünk meg. A kétváltozós
Karnaugh-tábla az ún. minterm tábla,
kombinációs szorzatait idézzük fel a következő ábrán:
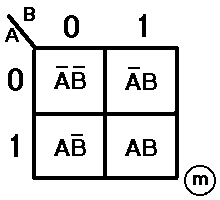
Minterm-nek nevezzük
a változókból ill. negáltjukból képzett logikai szorzatokat. Egy kétváltozós
függvénynek 4db mintermje lehet. Kettőnél több változó esetén a széleken
a számozáshoz több feltételt kell teljesítenünk: követelmény, hogy minden
mintermnek egy és csak egy helye legyen a Karnaugh-táblán – megtartva a
koordináták szerinti helykijelölés elvét.
Másrészt azért, hogy a táblát egyszerűsítésre
lehessen használni, a változók területeit úgy kell kijelölni, hogy
a mintermek szomszédosak legyenek: az egymás melletti sorok vagy
oszlopok csak egyetlen változóban térjenek el egymástól (nem lehet
például az egyik oszlopban két változó valódi
értékű, a mellette lévőben pedig mindkettő
negált értékű). Ezen elvek alapján a háromváltozós Karnaugh-tábla
8 rekeszű, a négyváltozós pedig 16 rekeszű
melyeket a következő ábra szemléltet:

Mivel a szomszédos oszlopok és sorok csak egy változóban térhetnek el egymástól a számozás nem bináris sorrendű, hanem egylépéses (GRAY) kód szerinti (mivel ilyen kód esetén a szomszédos számok csak egyetlen helyiértéken különböznek egymástól).
A függvényeket minterm-táblán úgy ábrázoljuk, hogy a függvény előállításában résztvevő mintermek rekeszébe 1-est (ez jelenti az igazságtáblázat azon sorait, amelyhez Y=1 tartozik), a többi rekeszbe pedig 0-t (vagy üresen hagyjuk, itt Y=0). A következő ábrán egy 3 változós függvény segítségével mutatjuk be, hogy milyen egyszerű az igazságtáblázatot Karnaugh-tábla formába átültetni:

A Karnaugh-táblás egyszerűsítés elve a közös tényező kiemelése. Mivel a széleken a változók koordinátáit egylépéses kódban jelöltük ki, a táblában bárhol két egymás melletti (alatti) cellában olyan mintermek vannak, amelyek “szomszédosak” azaz 1 változó kivételével azonosak. Ezt az azonos részt kiemelhetjük, a megmaradó változó és negáltja pedig “kiesik”, ahogyan ez a következő ábrából pontosan leolvasható:

A szomszédos mintermek összevonásakor természetesen nem írjuk le a teljes azonos átalakítást, hanem az összevonandó 1-eseket egy hurokkal vesszük körül és ezután már csak ennek a huroknak az eredményt tüntetjük fel. Ez nem lesz más, mint a hurok “közös”, megmaradó változóiból alkotott logika szorzat: példánkban az A változó 1-es a hurok mindkét eleménél, tehát A benne lesz a közös részben, a B az egyik helyen nulla a másikon egy, tehát “kiesik”, elhagyjuk, a C szintén 1-es értékkel jelen van mindkét mintermben, így tehát azonnal írhatjuk a hurokban végrehajtott összevonás eredményét: AC.
Ezzel a módszerrel nem
kell túl nagy szellemi energiát fordítanunk az összevonásra: a hurok közös
jellemzőit leírjuk, ami változik azt elhagyjuk. A grafikus egyszerűsítésnek
ez a nagy előnye: A szomszédos mintermek, vagyis az összevonási lehetőségek
azonnal észrevehetők és a (rész) összevonások
eredménye azonnal odaírható. Ábránkon látszik, hogy még egyéb egyszerűsítési
lehetőségek is vannak – feltéve, hogy a már egyszer felhasznált
ABC minterm 1-esét ismételten bevonhatjuk egy másik hurokba
is. Egy logikai függvényben egy tagot tetszés szerint ismételhetünk az
egyszerűsítés érdekében, így a Karnaugh-tábla bármely 1-esét is
akárhány hurokba bevonhatjuk.
A következő ábrán bejelöltük az összes egyszerűsítési lehetőséget (hurkot) és odaírtuk az eredményét is.
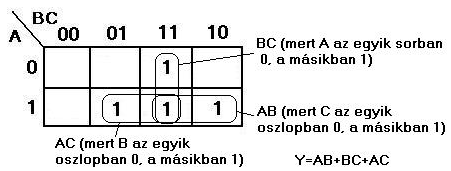
Az egyszerűsített függvényt a grafikus összevonások eredményeképpen kapott logikai szorzatok összege adja:
Tekintve, hogy a Karnaugh-táblában az egymás melletti rekeszek sor-ill.
oszlop irányban szomszédosak, nemcsak 2, hanem –
megfelelő egymás melletti alakzatban – 4,8…stb.
szomszédos term is összevonható, de minden esetben 2 egész számú hatványával
egyező darabszámú: ![]() n=1,2….
n=1,2….
Lehetséges összevonások a
Karnaugh-táblában a következők
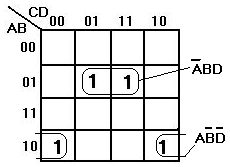
- 2 db egymás melletti (egymás alatti) 1-es összevonható. A tábla a széleken összefügg: egymás mellettinek ill. alattinak számítanak a sorok, ill. oszlopok két végén levő 1-esek is. Ilyenkor 1 változó kiesik.
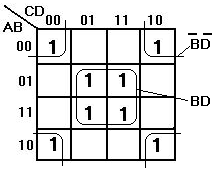
4db négyzet alakban elhelyezkedő 1-es összevonható (mivel az egymás melletti és alatti 1-esek szomszédosak). A négy sarokban lévő 1-es is négyzet alaknak számít. Ilyenkor két változó esik ki. Teljes sorok valamint teljes oszlopok összevonhatók (2 változó esik ki)
Két szomszédos teljes sor vagy oszlop összevonható (8 elem összevonásakor 3 változó esik ki Az egész tábla összevonható, ha egy feladat kapcsán kiderül, hogy valamennyi rekeszben 1-es van,ekkor Y=1